
【软考知识总结】数据结构和算法
前言
这一部分的内容除了选择题会出现,还有最后的大题涉及到算法设计和实现,主要内容就是大学时期讲的数据结构相关的内容,数组、链表、栈、队列、串以及常见的排序和搜索算法。
数据结构
数组
连续的存储空间,顺序的分配给数据结构,地址计算,本质是起始地址+前面的元素数量*长度
特殊矩阵
对称矩阵,a[i][j]=a[j][i],相当于对角线对称
对角矩阵,非零元素集中在对角线中心
三角矩阵,主对角线上方全是非零,下方全是零,或者反过来
稀疏矩阵
非零元素个数远少于零元素个数,且不规律
存的时候,可以直接存非零元素
广义表
普通线性表的元素只能是单元素或者单个子表,广义表可以部分元素是单元素,部分元素是子表
一般记为 LS = (a1, a2, …, an),深度就是最深的括号的个数,比如 LS = (1, (2, {3})),深度就是3,原子深度为0,空表深度为1
表头可能是单元素或者表,但表尾只能是表,因为表尾的定义是除去表头之外的其他元素组成的表

树
树的定义是,其中每一个元素可以有两个或以上的直接后继元素

二叉树

线索二叉树
线索二叉树,以比特标记位,利用那些空闲的指针保存前驱和后继,前驱和后继由遍历形式决定,比如前中后三种遍历方式中,前驱和后继的定义并不一致。

哈夫曼树
哈夫曼树代价的计算,叶子节点的权值*根节点到叶子节点的路径长度,并求和
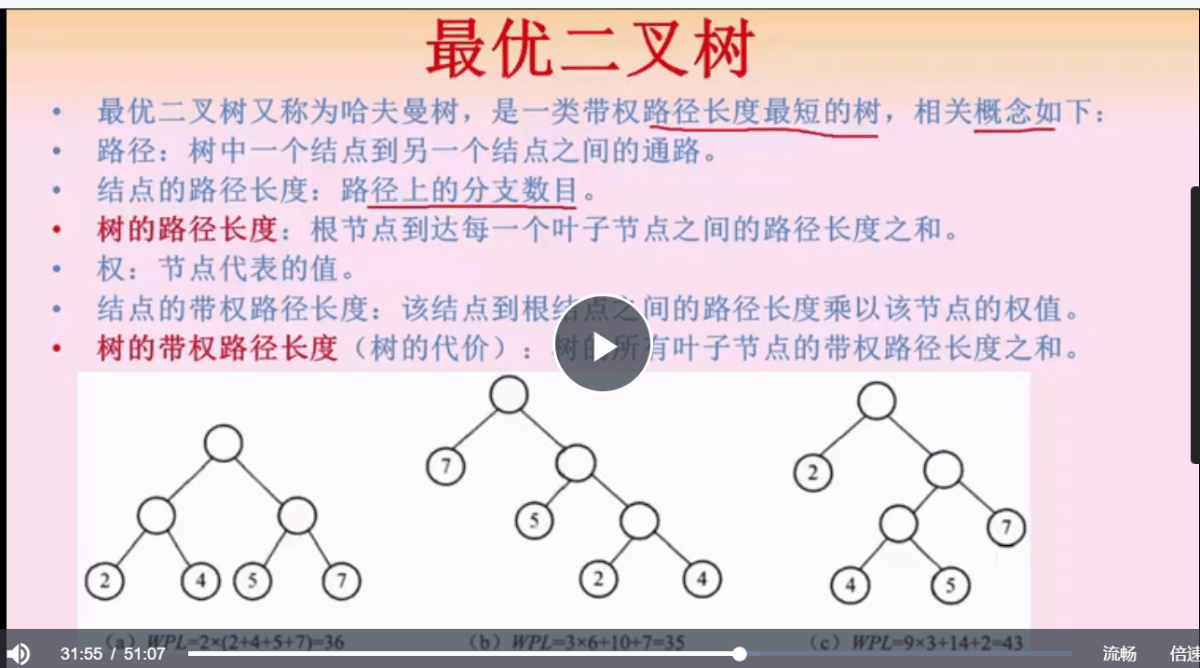
构建哈夫曼树的重点是,找两个最小的权值节点,加起来作为其父节点,然后把父节点放到集合中,再找两个最小的权值节点,循环往复即可。
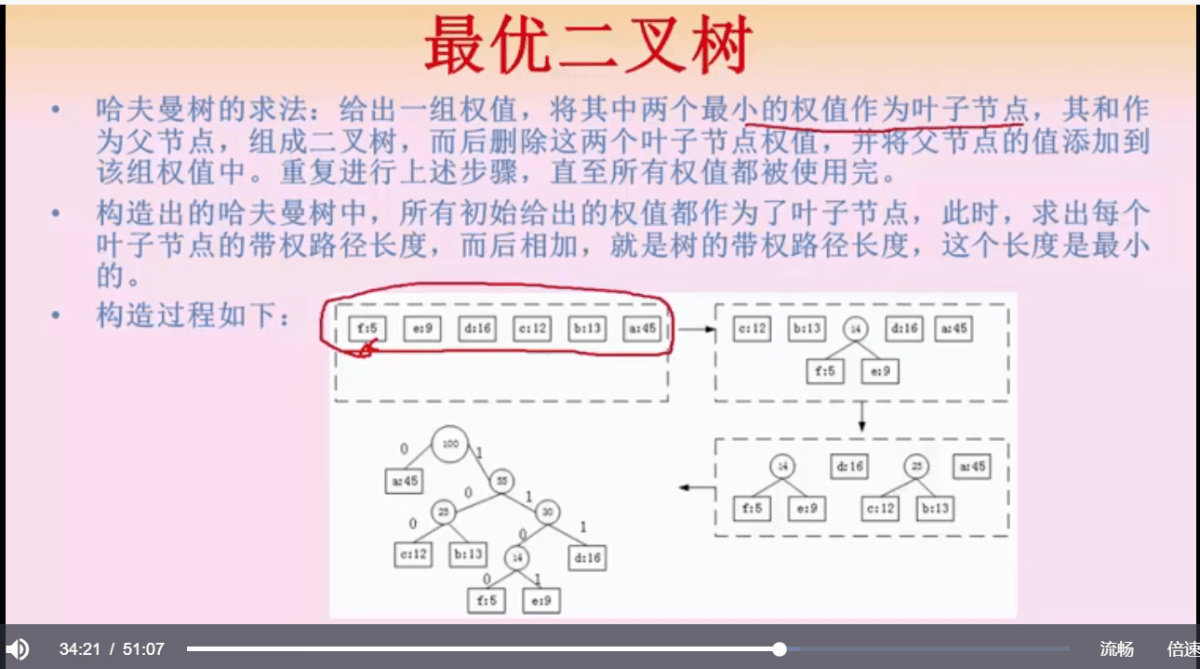
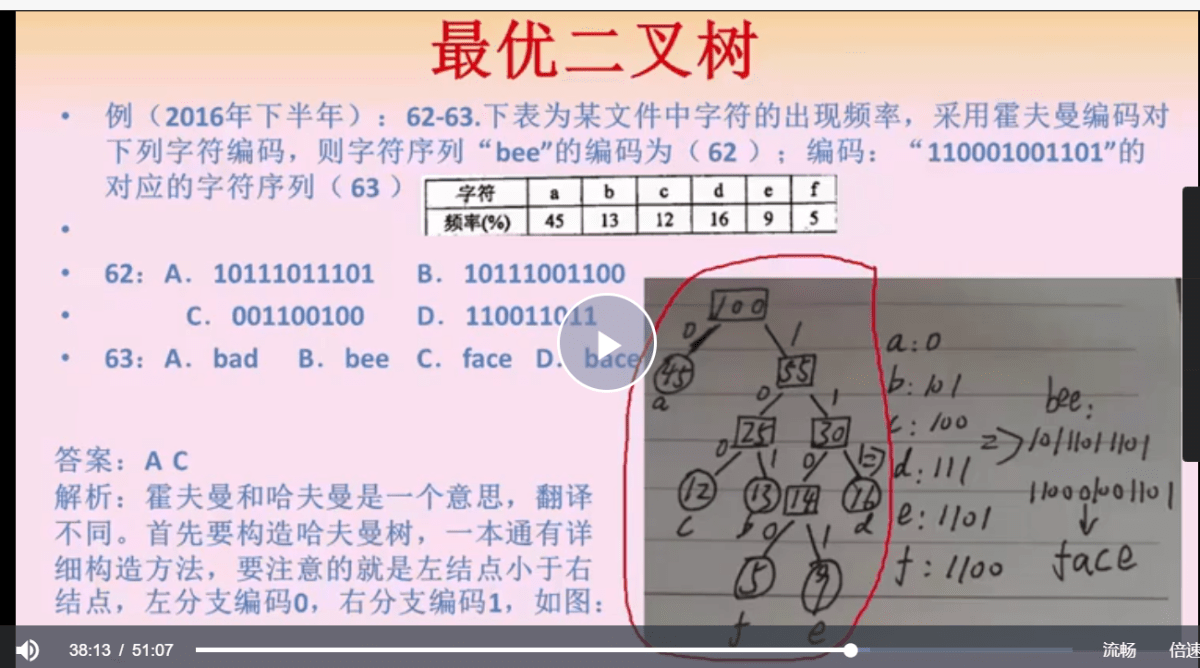
哈夫曼树编码的规则是往 左走是0,往右走是1,注意左边小右边大, 构造出来的哈夫曼树是唯一的,所以编码和解码也是唯一的。
树和森林
树和二叉树转换需要掌握
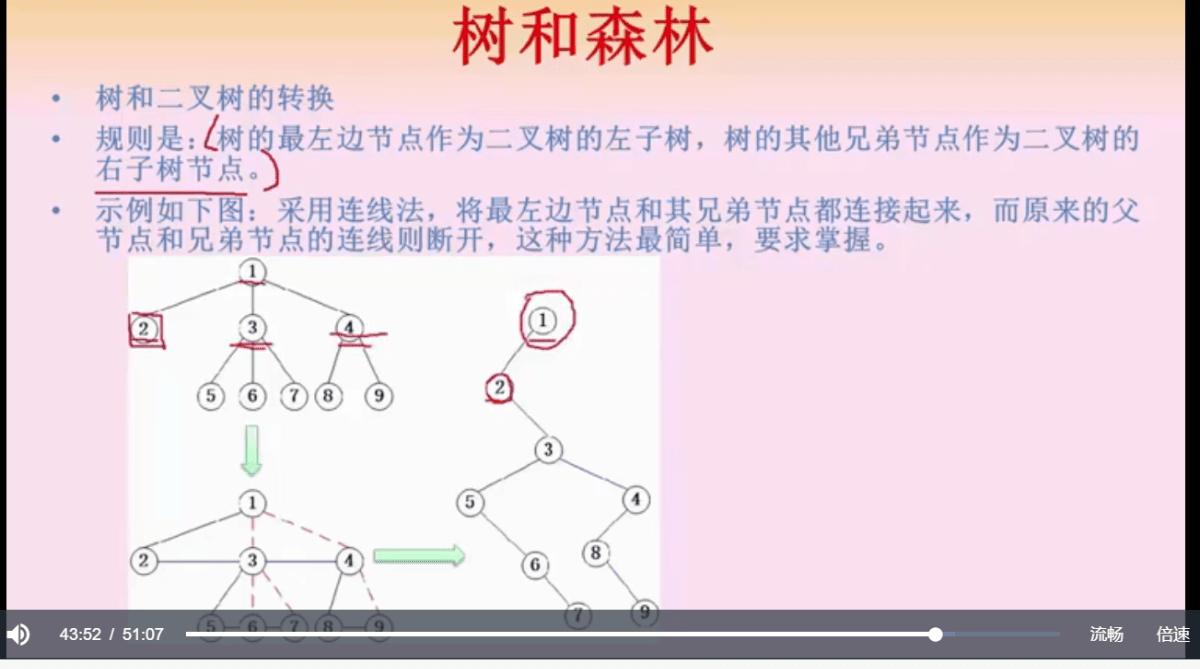
三叉树,主要是把最左边的节点单独拧出来,然后兄弟节点接到最左节点的右边顺着排,然后每个节点的左边就是其下最左的节点,右边就是兄弟,最左节点的规律等同。
还原的时候,也是先把左节点拧出来,然后兄弟列出来,再以同样的方式遍历兄弟节点的最左节点及其兄弟。

查找二叉树,根节点的选择很重要,树的深度影响效率
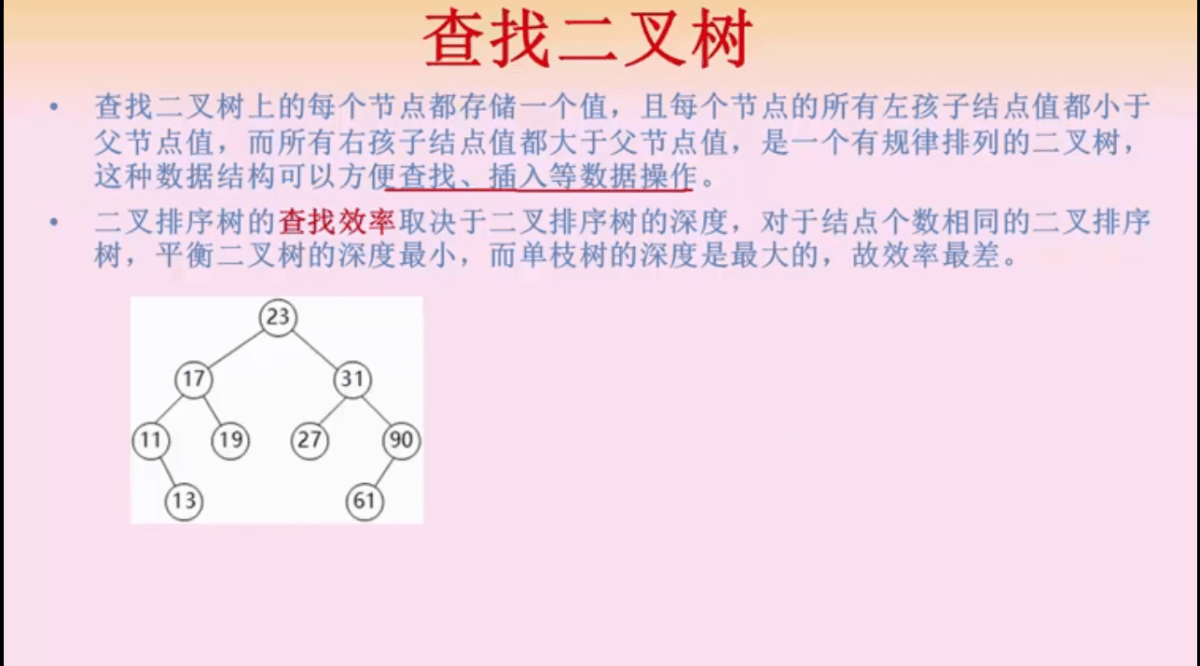
先序和中序反推树,先序确认根节点,中序确认左右子树,一定不要搞反了,确认根节点后,中序中在根节点前的位于其左边,内部的结构同样的,按照先序找到根节点,然后同样的规律求解。
图
图的定义:
无向图:无箭头,不分方向
有向图:有方向
完全图:无向完全图和有向完全图,无向完全图中,每个节点两两间都有连线,连线数量为 (n-1) + (n-2)+….1 = n*(n-1)/2,有向完全图的连线数量为无向完全图连线数量的两倍,n*(n-1)
度:顶点的度指的是与顶点相关的边的数量,有向图中由顶点指出以及指入顶点的边分别被称为出度和入度,顶点的度为两者之和。
路径:从一个顶点到另一个顶点的通路,有向图的路径带方向
连通图:如果无向图中所有顶点都是连通的就是连通图
连通分量:无向连通图中最大的连通子图就是连通分量
强连通图:有向图中所有顶点都是连通的图
强连通分量:有向连通图中最大的强连通子图就是连通分量
网:边带权值的图称为网

图的存储
邻接矩阵,arr[i][j] 表示节点 i 到 节点 j 有单向的通路,所以无向图是延对角线对称的,其数组对应的值也可自定义存储权值等信息
邻接表,arr[i] 表示节点 i 到其他节点有单向通路的链表,可附带存储权值等信息
适合采用什么形式,跟图的类型无关,跟节点数和连接数有关
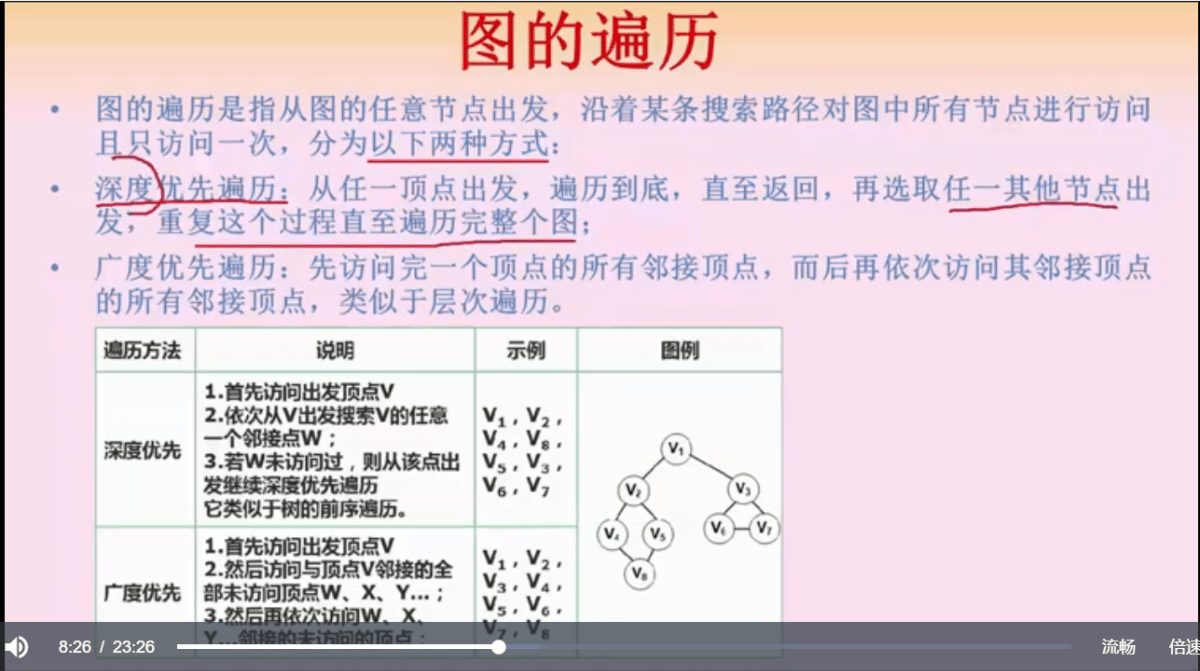
图的遍历
深度遍历,遍历到底,所以遍历结果不一定是一致的
广度遍历,一层层访问所有节点
图的最小生成树
用一个树把所有顶点连起来,树的边权值之和最小,那么这个树就是最小生成树
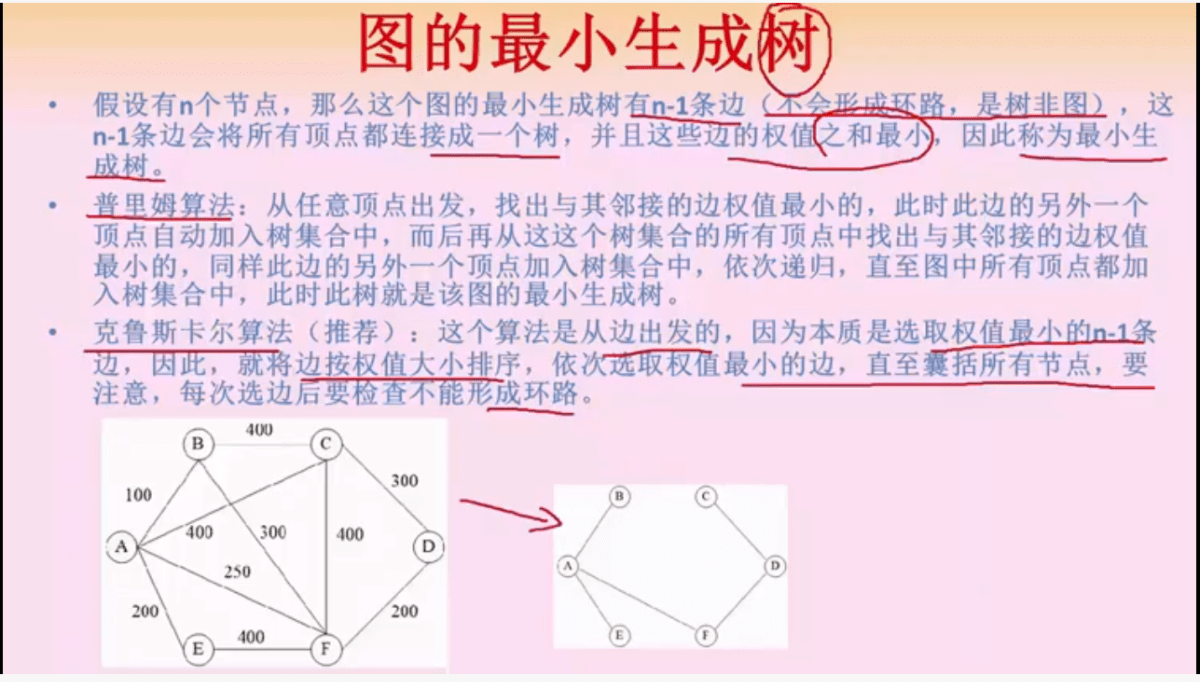
克鲁斯卡尔算法:把边按照权值排序,依次引用,碰到环的就排除,直到所有的节点被连接起来
普里姆算法:从任意顶点出发,找到最小边,然后把这条边对应的另一个顶点与初始顶点放入集合中,再从这个集合中找最小的边,重复操作直到把所有的顶点都连接起来
克鲁斯卡尔算法和普里姆算法都用了贪心的思维,普利姆算法因为每次都是从集合中的点往外扩散找新的点,所以所有的顶点只会有一个入度,就不会成环。
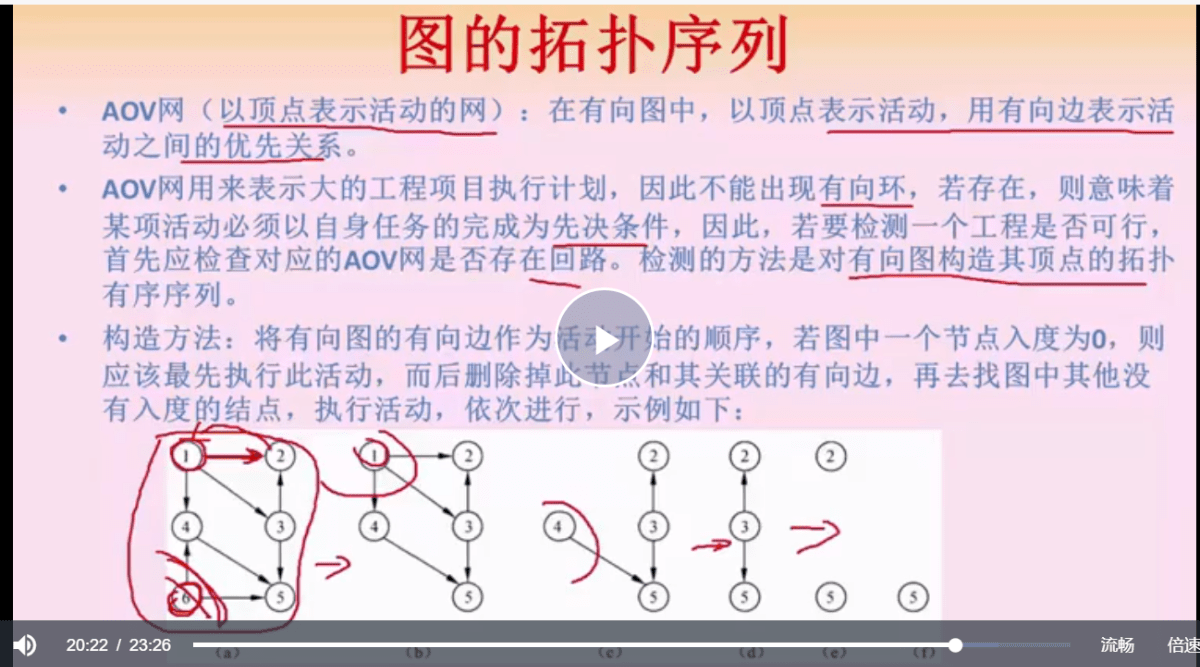
图的拓扑结构
其诞生是为了解决活动序列成环检测,因为作为一个活动执行计划来说,不能出现活动 A 依赖活动B 执行完毕,而活动 B 反向依赖活动 A 执行完毕,那不就死锁了
构造方法:找到入度为0的节点,然后删掉这个节点和这个节点所对应的边(表示执行这个节点的活动),然后继续找入度为0的节点,循环往复,如果能把所有的节点都删完,说明所有的活动都可以执行完毕,反之就存在环。
算法分析
重要特性
- 有穷性,有穷步骤,有穷时间
- 确定性,相同输入得到相同输出
- 可行性,算法中的操作需可行
- 输入,零个或多个输入
- 输出,一个或多个输出
查找
- 顺序查找,O(n)
- 二分查找,已排序的情况,O(logn)
- hash查找
排序
- 稳定,不稳定
- 内和外

排序算法
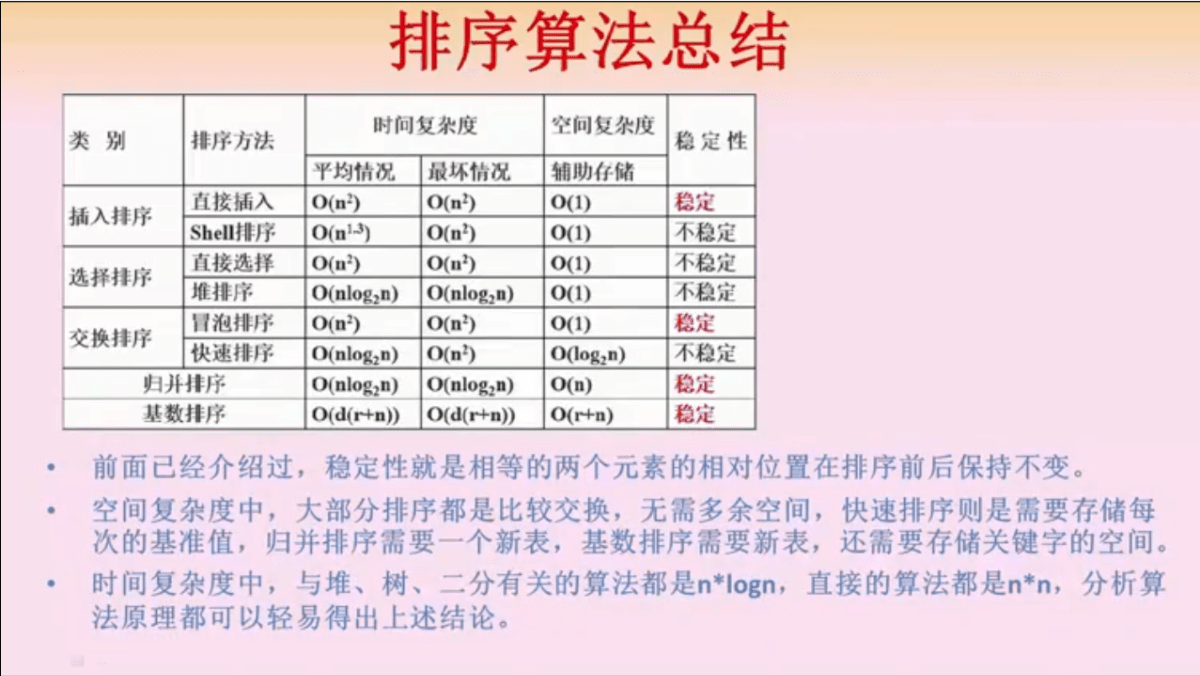
插入排序,顺序序列找到比较合理的位置插入,稳定排序
希尔排序,对大量数据进行分组(按照增量序列分组),每个组内进行插入排序,然后所有的组再进行大的插入排序,同时操作的数据量级可控,适合大量数据排序
简单选择排序,找到合理的数据进行交换,不稳定排序
堆排序,初始化一个大/小顶堆,然后不停的取堆顶,调整堆结构,进而得到顺序的序列,适用于得出仅前几名的场景,效率比较高
冒泡排序,看起来比简单选择交换的数据多,但这是稳定排序
快速排序,给一个基准,左边小于基准,右边大于基准
- 两个指针,尽可能减少基准和指针数据的交换
归并排序,从子序列长度为1的分组归并开始,一步步的把所有数据排到一个集合内,适合线性表,大文件的排序等
基数排序,多关键字排序,一般是数据特别庞大的时候适用,比如个位、十位、百位做三轮排序,然后从大到小找出结果
推排序的重点
先用二叉树把元素顺序排列好,然后通过大/小顶堆的规则初始化一个堆,取堆顶元素就是一个最值,然后把叶子节点放到堆顶 ,再根据大/小堆的规则进行调整,直到取出自己想要的数量。
只有插入、冒泡、归并和基数是稳定排序,其他的都是不稳定排序

算法理论
分治法:分解为多个独立子问题进行处理,子问题互相独立,并与原问题形式相同
回溯法:系统性的搜索所有的解,深度优先搜索可能解的树
动态规划法:划分子问题,并保证每一个子问题最优,且全局最优
贪心法:划分子问题,子问题是最优的,不考虑全局,不用穷举所有解,但相对性能比较好,不一定能得到最优解
分支限界法:跟回溯法的区别在于,列出所有子情况并抛弃不合理的情况,并非回溯法走深度遍历,相当于广度优先遍历
概率算法:随机选择下一步,能接受一定的错误,能很快出解
近似算法:放弃最优解,使用近似最优解,换取时间和空间复杂度
数据挖掘
爆炸式增长的数据进行分析和信息挖掘,核心是算法
主要功能包含,分类,回归,关联和聚类
考点:
分类是有监督的学习过程
聚类是无监督的学习过程
频繁模式和关联规则挖掘,从频繁模式出发,找到其中关联规则,进而发现交叉销售机会

智能优化算法
以数学为基础,求解工程中优化解的应用技术,包括:
ANN,人工神经网络
深度学习
遗传算法,基于自然的演化机制
SA,退火算法,求解全局优化算法,模拟加温、等温、冷却
TS,禁忌搜索算法,有点贪心的思维,局部近邻搜索的扩展
蚁群算法,寻找优化路径的概率型算法,模拟蚁群寻找食物最短路径,留下类似信息素的信号,形成一个类似正反馈的机制
鸟群觅食法,模拟鸟群飞行时整体方向一致
- 跟踪个体/全局的极值,通过迭代找到最优解

总结
数据结构需要掌握其原理和多种表现形式,算法需要了解其核心逻辑以及特点